C++ Materials
Here is a small program to change from Infix to Postfix notation written in C++.
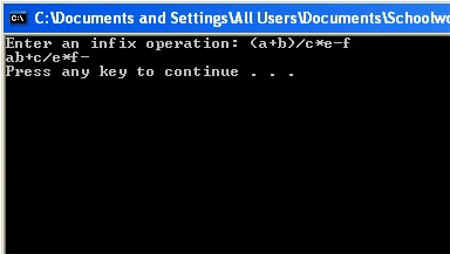
Click here if you would like obtain the source for this program.
Here is a small program to change from Postfix to In- and Prefix notation written in C++.
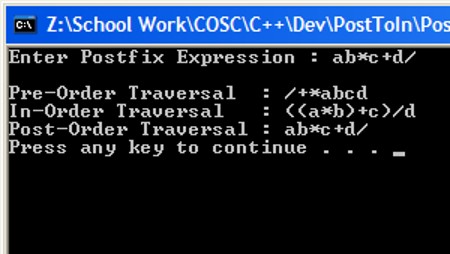
Click here if you would like obtain the source for this program.
A GCD-program written in C++.
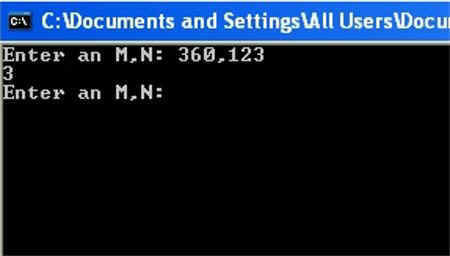
Click here if you would like obtain the source for this program.
A CDF-program written in C++.
This code implements a function that calculates the standard normal CDF (x), usingan approximation from Abromowitz and Stegun Handbook of Mathematical Functions.
Click here if you would like obtain the source for this program.
Four Integer Factorization-program written in Java.
These code implements functions that breaks down a composite number into smaller non-trivial divisors.By the fundamental theorem of arithmetic every positive integer has a unique prime factorization. Implemented
here are four algorithms for such factorization, Fermat's factorization method, Shank's Square Form, Pollard's
Rho and Pollard's p-1 algoritms. Java is used due to the built-in BigInteger functions.
Click here
if you would like obtain the source for Fermat's factorization method.
Click here
if you would like obtain the source for Pollard's Rho algorithm.
Click here
if you would like obtain the source for Pollard's p-1 algoritm.
Click here
if you would like obtain the source for Shank's Sqaure Form algoritm
Richardson's Extrapolation Algorithm written in C++.
This program implements Richardson's algorithm to find the derivative at a certain point.
Click here if you would like obtain the source for this program.
Romberg's Integration Algorithm written in C++.
This program implements Romberg's algorithm to integrate a function over a given length.
Click here if you would like obtain the source for this program.